Sempre quando estiver realizando uma análise epidemiológica e a associação entre variáveis estiver presente é possível quantificar a magnitude da diferença de chance ou de risco. Para isto, em epidemiologia, usamos duas medidas para nos apoiar nesta análise:

• O Risco Relativo (RR) e
• O Odds Ratio (OR).

Nas subseções logo abaixo iremos rever os conceitos e aprender a aplicá-los no dia a dia, dando robustez às análises realizadas e qualificando ainda mais a rotina de análise dos serviços de vigilância em saúde municipais.

O Risco Relativo é uma razão de incidências que estima a magnitude das diferenças de incidência entre os grupos expostos e não expostos a um fator e a ocorrência da doença.

Em poucas palavras, calcular o valor do RR expressa quantas vezes é maior (ou menor) o RISCO de desenvolver a doença no grupo que foi exposto a um determinado fator em comparação a um grupo que não foi exposto. Expressa uma comparação matemática da incidência entre os grupos. Veja seu cálculo matemático:

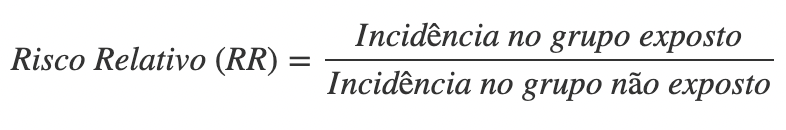
• Quando o resultado dessa comparação é igual a 1: indica que a incidência da doença no grupo exposto é igual à do grupo não exposto, portanto não há associação entre exposição e doença.

• Quando o resultado é maior que 1: indica associação positiva ou risco aumentado entre os expostos ao fator estudado (potencial fator de risco).

• Quando o resultado é menor que 1: indica um risco diminuído entre os expostos ao fator estudado (potencial fator de proteção).

Para analisar esta situação, observe a tabela abaixo que faz uma simulação de grupos expostos e não expostos (na linha) e se houve ou não a doença (na coluna). As letras expressam as seguintes interseções:

• Pessoa que foi exposta e ficou doente: letra “a”;
• Pessoa que foi foi exposta e não ficou doente: letra “b”;
• Pessoa que não foi exposta e ficou doente: letra “c”;
• Pessoa que não foi exposta e não ficou doente: letra “d”.

Logo, a incidência da doença em quem foi exposto é representada por a/a+b e a incidência da doença em quem não foi exposto é representada por c/c+d.

Figura 4: Tabela 2x2 para avaliação do Risco Relativo.

A partir da tabela acima o cálculo do Risco Relativo seria o seguinte:

Agora, vamos praticar no R utilizando um exemplo comum na rotina de vigilância em saúde!

Considere que você foi chamado para participar da investigação de um surto de gastroenterite (DTA) entre pessoas que participaram de uma festa de casamento. Ao total, 80 pessoas estiveram presentes no jantar que ocorreu em uma igreja no dia 18 de abril. O jantar foi realizado das 18 às 23 horas. Durante este período, os alimentos ficaram expostos em uma mesa e disponíveis aos convidados.

A equipe da Vigilância Epidemiológica de Rosas conseguiu entrevistar 75 pessoas, sendo coletados os seguintes dados:

• alimentos que foram consumidos pelas pessoas;
• se a pessoa ficou doente (considerando a definição de caso prevista para o surto);
• a hora do jantar;
• o dia e hora do início dos sintomas;
• a idade e o sexo das pessoas.

Os dados coletados foram tabulados e enviados ao seu e-mail no formato texto (.csv). Agora você deverá seguir o passo a passo abaixo para analisá-los:

1. Importaremos o banco de dados {base_surto.csv}, localizada no menu lateral “Arquivos”, do módulo. Agora iremos analisá-lo com auxílio do R, replique o script abaixo em seu RStudio:

# Carregando o banco de dados do surto e criando uma tabela (dataframe) com o nome 
# base_surto
base_surto_18_04 <- read_csv("Dados/base_surto.csv")

#> Rows: 75 Columns: 21
#> ── Column specification ────────────────────────────────────────────────────────
#> Delimiter: ","
#> chr  (17): sexo, doente, data_inicio_sintomas, presunto, espinafre, pure_bat...
#> dbl   (2): id, idade
#> time  (2): hora_jantar, hora_inicio_sintomas
#> 
#> ℹ Use `spec()` to retrieve the full column specification for this data.
#> ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

Como já deve ser de seu conhecimento, a investigação de surto pela vigilância visa constatar a causa do surto, suas características quanto ao local, pessoa e tempo e quais ações necessárias para seu término. Considere também que a análise pode determinar se existe alguma associação entre consumo de algum alimento e a ocorrência da doença. Portanto, vamos construir as tabelas 2x2 para cada um dos supostos fatores de risco.

2. Como recurso estético, vamos deixar a tabela um pouco mais compacta, executando a função theme_gtsummary_compact(), considerando que a tabela pode ficar grande e de difícil visualização.

3. Vamos retirar as variáveis que não vamos utilizar neste momento utilizando a função select(). Note que estamos utilizando o símbolo de menos (-) para retirar as variáveis de identificação (id), data e hora de início de sintomas e hora do jantar.

4. Em seguida, utilizaremos a função tbl_summary() do pacote gtsummary apresentada anteriormente. Faremos um cruzamento entre as variáveis sobre alimentos ingeridos e a variável com status da doença.

5. E como último passo aplicaremos a função add_p() para o cálculo do teste estatístico adequado para verificar se há associação entre os fatores e o status dos doentes.

Executaremos agora juntos os passos 2 a 5, escrevendo-os no script abaixo:

# Utilizando a função theme_gtsummary_compact() para facilitar a visualização da 
# tabela que será gerada
theme_gtsummary_compact()

base_surto_18_04 |>
  
  # Removendo as colunas id, data_inicio_sintomas, hora_inicio_sintomas e 
  # hora_jantar com a função select()
  select(-id,
         -data_inicio_sintomas,
         -hora_inicio_sintomas,
         -hora_jantar) |>
  
  # Criando uma tabela com resumo das informações de acordo com a coluna "doente"
  tbl_summary(by = doente, missing = "no") |>
  
  # Adicionado o p-valor com a função add_p()
  add_p()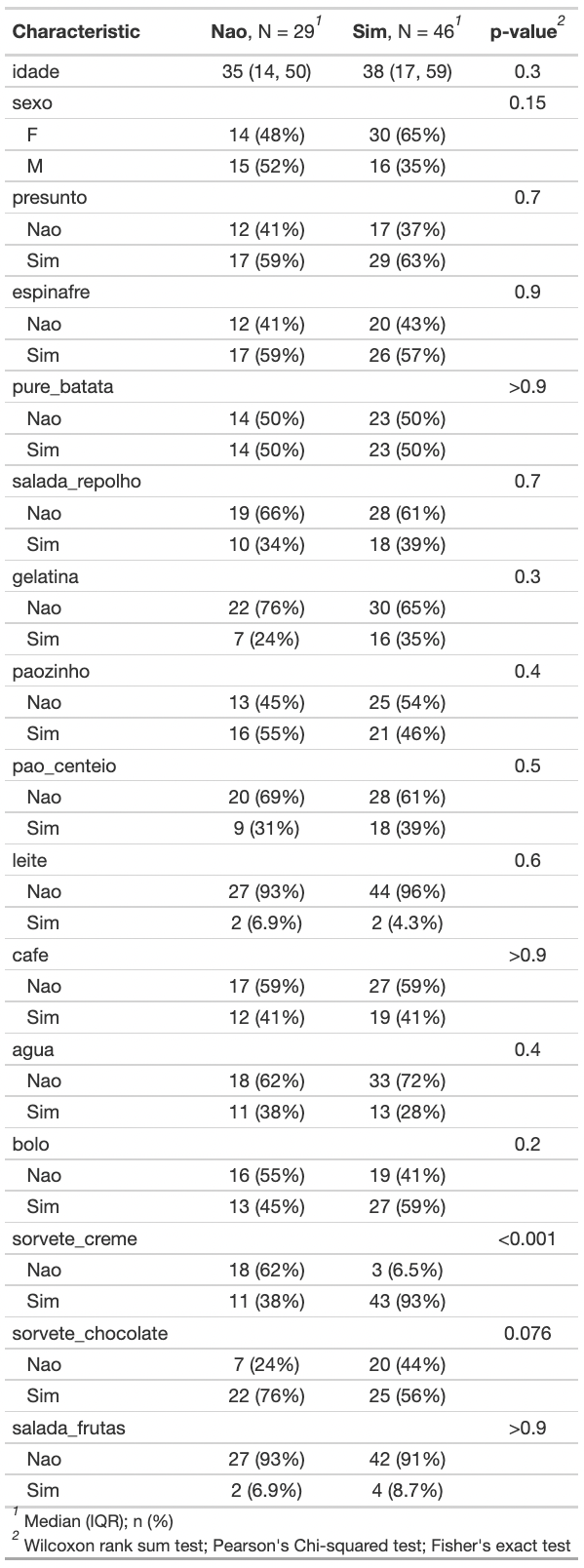

Pronto, verifique se os seguintes resultados para os que ficaram doente foi o seguinte:

• 65% eram mulheres e com 38 anos de idade mediana.
• Alguns alimentos não foram muito consumidos por este grupo como salada de repolho (61%), pão de centeio (61%), gelatina (65%), água (72%), salada de frutas (91%) e leite (96%).
• Por outro lado, a maioria das pessoas que consumiram o sorvete de creme desenvolveram gastroenterite (93%).

Nessa situação, perceba que o sorvete de creme é o único alimento que as pessoas foram “expostas” e que apresentou valor de p menor que 0,05 no teste estatístico de associação. Temos, portanto, nosso principal suspeito. Perceba também que, agora, será preciso comparar quem foi exposto ou não ao fator de risco (sorvete de creme) e que desenvolveram a doença (gastroenterite) ou não. Vamos calcular o Risco Relativo (RR)!

6. Para calcular o RR, vamos precisar do pacote epitools, muito útil para cálculo de medidas de associação e já carregado no início do módulo.

7. Para o cálculo do Risco Relativo vamos utilizar a função riskratio() do pacote epitools. Essa função possui três argumentos principais:

   • x: vetor contendo os números da tabela 2x2;
   • method: método para calcular o Risco Relativo. Usaremos o método de Wald;
   • rev: ordem das linhas e colunas que serão realizados os cálculos. Usaremos “both”.

O argumento conf.level define o nível de confiança das estimativas. Por padrão ele já é preenchido como 0,95 (95%). Assim, não é necessário inseri-lo na função. Caso queira alterar, basta definir na função com o valor correspondente.

Vejamos como implementamos o cálculo do RR para o sorvete de creme. Vamos inserir o vetor com os dados do sorvete de creme na função riskratio(), com os argumentos citados acima. Vamos salvar o resultado em um objeto chamado resultado_rr.

Acompanhe o script abaixo e replique-o em seu RStudio:

# Calculando o risco relativo com a função riskratio() e criando um objeto do
# com o nome resultado_rr_surto
resultado_rr_surto <- riskratio(x = c(43, 11, 3, 18),
                                method = "wald",
                                rev = "both")

8. O objeto resultado_rr que retorna da função é um objeto do tipo lista composta por quatro itens: os dados (data), o cálculo do risco relativo com intervalo de confiança (measure), o p valor (p.value) e correção (correction), ou seja, se houve correção estatística. Você os estudará de forma detalhada mais a adiante. Agora, escreva os comandos abaixo em seu RStudio:

# Visualizando os nomes do objeto resultado_rr_surto
resultado_rr_surto

#> $data
#>           Outcome
#> Predictor  Disease2 Disease1 Total
#>   Exposed2       18        3    21
#>   Exposed1       11       43    54
#>   Total          29       46    75
#> 
#> $measure
#>           risk ratio with 95% C.I.
#> Predictor  estimate   lower    upper
#>   Exposed2 1.000000      NA       NA
#>   Exposed1 5.574074 1.93834 16.02934
#> 
#> $p.value
#>           two-sided
#> Predictor    midp.exact fisher.exact   chi.square
#>   Exposed2           NA           NA           NA
#>   Exposed1 2.698215e-07 2.597451e-07 1.813314e-07
#> 
#> $correction
#> [1] FALSE
#> 
#> attr(,"method")
#> [1] "Unconditional MLE & normal approximation (Wald) CI"

Observe que os itens principais, visualizados, são:

-   `data`: contém a matriz com os dados utilizados.
-   `measure`: matriz com o resultado dos cálculos do risco relativo com intervalo 
de confiança.
-   `p.value`: matriz com resultados dos valores de p dos testes estatísticos 
realizados.

9. Como vamos precisar apenas dos cálculos do Risco Relativo (RR), vamos utilizar somente o segundo elemento da lista, chamado “measure”. Veja no script abaixo como o acessamos e replique-o em seu computador:

# Selecionando o objeto "measure" da lista resultado_rr_surto
resultado_rr_surto[["measure"]]

#>           risk ratio with 95% C.I.
#> Predictor  estimate   lower    upper
#>   Exposed2 1.000000      NA       NA
#>   Exposed1 5.574074 1.93834 16.02934

Agora podemos interpretá-lo. Considerando os padrões da tabela 2x2, a primeira linha foi a referência considerada para o cálculo dos expostos.

Assim, uma forte associação entre consumo de sorvete de creme e gastroenterite foi constatado, pois o valor do RR é maior que 1. Ou seja, pessoas que consumiram sorvete de creme apresentaram 5,57 vezes o risco de desenvolver gastroenterite, em comparação a quem não consumiu o sorvete.

Ufa! Conseguimos calcular o RR com sucesso. Agora vamos aprender a calcular o Odds Ratio!!

Odds ratio (OR) é uma razão que estima quantas vezes é maior (ou menor) a CHANCE de exposição a um determinado fator no grupo que já manifestou a doença em relação a um grupo não doente. Ou seja, odds ratio identifica a associação entre a exposição e doença entre pessoas que já desenvolveram a doença.

O termo odds se refere à probabilidade em português, mas alguns autores traduzem como “chance” e tem como sinônimos “razão de chances”, “razão de produtos cruzados” ou simplesmente “OR”, quando há a divisão das chances.

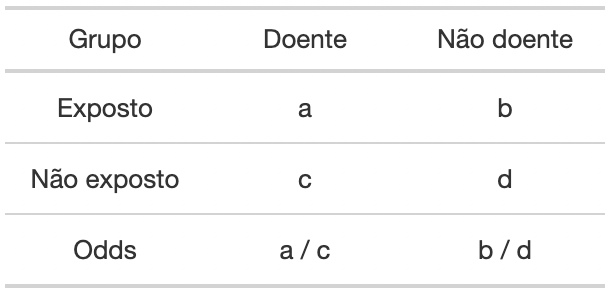
Remetendo a tabela 2x2, vamos novamente simular uma situação de exposição a um fator de risco e manifestação da doença. Observe abaixo como se apresentam as interseções:

• Pessoas que manifestaram a doença e foram expostas ao fator de risco: letra “a”;
• Pessoas que não manifestaram a doença e foram expostas ao fator de risco: letra “b”;
• Pessoas que manifestaram a doença e não foram expostas ao fator de risco: letra “c”;
• Pessoas que não manifestaram a doença e não foram expostas ao fator de risco: letra “d”.

Logo, a chance de ter sido exposto dado que manifestou a doença é representada por a / c e a chance de ter sido exposto dado que não manifestou a doença é representada por b / d.

Figura 5: Tabela 2x2 para avaliação do Odds Ratio.

A partir da tabela acima, o cálculo da OR, envolvendo as odds, pode ser expresso matematicamente da seguinte forma:

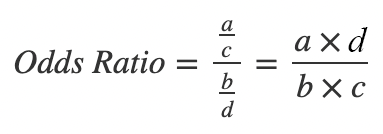
• Quando o resultado dos cálculos da OR for igual a 1, indicará a ausência de associação entre exposição e doença,
• Quando a exposição ao fator de investigação aumenta a chance de se apresentar a doença, a OR será maior que 1, e
• Quando a exposição ao fator age negativamente na doença, comportando-se como um possível fator de proteção, a OR será menor que 1.

Vamos praticar! Considere que enquanto profissional de vigilância, você precisará avaliar a situação da coinfecção entre tuberculose e HIV em casos do Estado do Acre! O adoecimento de tuberculose em pessoas vivendo com HIV (PVHIV) pode ser maior do que quando comparamos com outras pessoas não infectadas pelo vírus do HIV, principalmente pela influência da imunossupressão tornando esse grupo um dos mais vulneráveis, dentre os casos de tuberculose.

Levando em consideração esta premissa, você deverá analisar se há associação entre as pessoas com diagnóstico de tuberculose que vivem com HIV e o classificação do encerramento dos casos (desfecho). Para isso, imagine que você exportou o banco de dados de tuberculose do Sinan Net contendo todos os casos notificados entre anos de 2006 e 2020 no Acre. Este banco foi exportada no formato de arquivo “.dbf”.

Nesta situação, as pessoas já apresentaram a doença. Afinal, a notificação de casos de tuberculose se dá a partir da confirmação e não da suspeita. Dessa forma, precisamos identificar uma associação entre pessoas que manifestaram a tuberculose (doença) e estiveram ou não expostos ao fator de risco (HIV). Conduziremos os cálculos para com o apoio da medida de associação odds ratio.

Acompanhe o passo a passo da construção desta análise no script abaixo e replique-o no seu RStudio:

1. Primeiro, iremos importar os dados {base_tb_ac.dbf} que serão analisados para o ambiente do RStudio. Estes estão no menu lateral “Arquivos”, do módulo. Observe o script abaixo e replique o código em seu RStudio:

# Importando os dados {`base_tb_ac.dbf`} e armazenando 
# no objeto (dataframe) de nome {`base_tb`}
base_tb <- read.dbf(file = 'Dados/base_tb_ac.dbf')

2. Para facilitar nossa análise, selecione apenas as variáveis relacionadas ao objetivo. Utilize, portanto, a função select() do pacote dplyr para selecionar estas variáveis. Consultando o dicionário de dados do Sinan Net, serão necessárias para esta análise as variáveis:

   • SITUA_ENCE, que corresponde à situação do caso no momento do encerramento do caso e;

   • HIV, que se refere ao resultado da sorologia para o vírus da imunodeficiência adquirida.

Acompanhe o código abaixo, e replique-o em seu RStudio:

# Selecionando apenas as colunas HIV e SITUA_ENCE
base_tb <- base_tb |> select(HIV, SITUA_ENCE)

3. Agora, para comparar os grupos categorize as variáveis selecionadas. No dicionário de dados da tuberculose, percebe-se que a variável SITUA_ENCE possui 10 categorias codificadas conforme a tabela abaixo. Dessa forma, categorize em 2 grupos considerando o seguinte:

   • Registros de casos codificados como “1” serão categorizados como Desfecho favorável e;
   • Registros de casos codificados como “2”, “3”, “7”, “9” e “10” serão categorizados como Desfecho desfavorável.
   • Registros de casos com as demais evoluções não serão consideradas por não estarem relacionadas diretamente à tuberculose.

Observe na Figura 6 como ficou a categorização da variável SITUA_ENCE em formato de tabela, a partir das definições pactuadas acima. Observe a transformação do número dos códigos para as suas respectivas categorias:

Figura 6: Tabela de categorização da variável SITUA_ENCE.

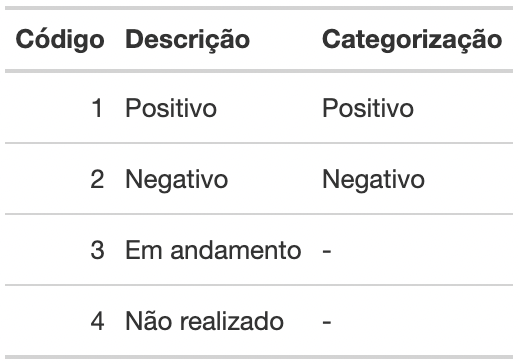
4. Agora, vamos categorizar também a variável HIV, conforme tabela abaixo (Figura 7). Observe que iremos descartar as variáveis que não revelam o resultado da sorologia. Pos estamos fazendo uma avaliação dos desfechos que aconteceram logo os casos em brancos não serão utilizados.

Figura 7: Tabela de categorização da variávelHIV.

5. Utilizaremos a função case_when() dentro da função mutate() para ambas categorizações.

6. Perceba que, na sequência, também faremos a transformação das variáveis para fatores com seus respectivos níveis (levels).

Acompanhe com atenção o código abaixo referente ao passos de 1 a 6 e reproduza este script no seu RStudio:

# Atualizando o objeto base_tb com as alterações que serão feitas
base_tb <- base_tb |>
  
  # Utilizando a função mutate() para criar novas colunas
  mutate(
    
    # Transformando os códigos de situação de encerramento nos nomes correspondentes 
    #com a função case_when()
    SITUA_ENCE = case_when(
      SITUA_ENCE == "1" ~ "Favorável",
      SITUA_ENCE %in% c("2", "3", "7", "9", "10") ~ "Desfavorável",
      TRUE ~ NA_character_
    ),
    
    # Transformando os códigos de resultado de HIV nos nomes correspondentes com a 
    # função case_when()
    HIV = case_when(HIV == "1" ~ "Positivo",
                    HIV == "2" ~ "Negativo",
                    TRUE ~ NA_character_),
    
    # Convertendo as colunas SITUA_ENCE e HIV em variáveis do tipo factor
    SITUA_ENCE = factor(SITUA_ENCE, levels = c("Desfavorável", "Favorável")),
    HIV = factor(HIV, levels = c("Positivo", "Negativo"))
  )

7. Agora, avalie a associação entre as variáveis por meio do teste estatístico qui-quadrado numa tabela 2x2:

   • Definindo hipótese nula como não associação entre Sorologia de HIV e situação do encerramento e o nível de significância do teste estatístico em 0,05.

Acompanhe os scripts abaixo e replique-os em seu RStudio

base_tb |>
  
  # Criando uma tabela de resumo do cruzamento de informações sobre
  # resultado para HIV e situação de encerramento
  tbl_cross(
    row = HIV,
    col = SITUA_ENCE,
    percent = "row",
    missing = "no"
  ) |>
  
  # Adicionado o p-valor com a função add_p()
  add_p()

#> FALSE observations with missing data have been removed.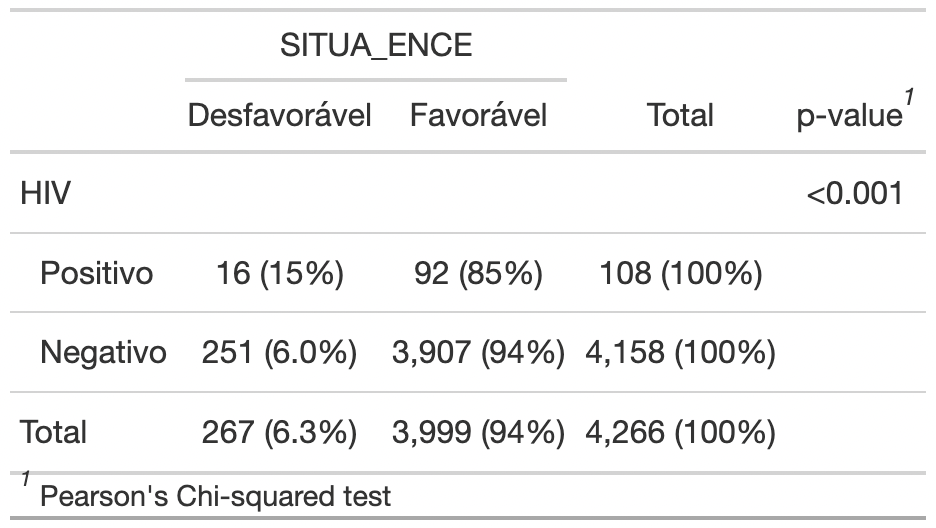

Pronto! Terminamos a primeira etapa do estudo de Odds Ratio. Agora vamos lá responder à pergunta: Existe associação entre pessoas com diagnóstico de tuberculose e vivem com HIV e a situação do caso no encerramento?

Analisando a tabela, é possível notar que na última linha, a porcentagem de desfechos desfavoráveis é de 6,3% mas, quando a sorologia de HIV é positiva (ou seja, a pessoa foi exposta ao fator de risco), esse valor vai para 15%. Analisando por outro lado, o desfecho favorável para tuberculose, que é a Cura, diminui quando a sorologia da pessoa é positiva para HIV. Constatamos assim, que há diferença entre os grupos avaliados.

Nota-se ainda que o valor de p foi menor que 0,05, evidenciando que a hipótese nula pode ser rejeitada. Isso significa que há evidência para associação entre desfecho desfavorável para pessoas com tuberculose e quando expostas ao vírus HIV.

8. Seguindo a análise, precisaremos mensurar a magnitude dessa associação. Para o cálculo da odds ratio vamos utilizar a função oddsratio() do pacote epitools. Essa função é muito parecida com a função apresentada anteriormente e possui os mesmos argumentos principais:

• x: vetor contendo os números da tabela 2x2;
• method: método para calcular a odds ratio. Usaremos o método de Wald;
• rev: ordem das linhas e colunas que serão realizados os cálculos. Usaremos “both”.

Vamos inserir o vetor com os dados da tabela 2x2 acima, sem os totais. Vamos salvar o resultado em um objeto chamado resultado_or_tb.

Replique o script abaixo em seu RStudio:

# Calculando o oddsratio com a função oddsratio()
resultado_or_tb <- oddsratio(x = c(16, 92, 251, 3907),
                             method = "wald",
                             rev = "both")

9. Agora vamos visualizar os resultados do cálculo da odds ratio:

Acompanhe o script abaixo e replique em seu RStudio:

# Selecionando o objeto "measure" da lista resultado_or_tb
resultado_or_tb[["measure"]]

#>           odds ratio with 95% C.I.
#> Predictor  estimate    lower    upper
#>   Exposed2 1.000000       NA       NA
#>   Exposed1 2.707085 1.568086 4.673409

Considerando os padrões da tabela 2x2, a primeira linha foi a referência considerada para o cálculo dos expostos. Assim, os cálculos nos levam a concluir que parece haver uma forte associação entre pessoas com tuberculose vivendo com HIV e desfecho desfavorável de tuberculose, pois o valor da OR é maior que 1. Ou seja, pessoas que vivem com HIV apresentaram 2,7 vezes a chance de terem desfechos desfavoráveis de tuberculose em comparação àqueles que não foram expostos ao vírus.