4. Análises de variáveis categóricas
Na análise exploratória em saúde, quando avaliamos duas variáveis categóricas, ou seja, variáveis qualitativas categorizadas em classes (por exemplo: variável sexo, categoria: feminino e masculino), o resumo dos dados se dá por meio da contagem de indivíduos que pertencem às categorias de ambas as variáveis, simultaneamente.
Para isto, costumamos montar tabelas de análises chamadas de tabelas 2x2 ou tabelas de contingência. Muito utilizadas quando calculamos taxa de ataque, uma espécie de coeficiente ou taxa de incidência que analisa uma determinada doença comparando um grupo de pessoas expostas ao mesmo risco limitadas a uma área bem definida. O cálculo da taxa de ataque é muito útil para investigar e analisar surtos de doenças ou agravos à saúde em locais delimitados.
Na representação abaixo utilizaremos um exemplo em que iremos verificar se um grupo de pessoas em um município possui maior chance de adoecer e após ter frequentado um restaurante com suspeita de contaminação nos alimentos. Desta forma, temos duas variáveis (“estado de saúde” e “restaurante”), e duas categorias em cada uma (saudável/doente, e frequentou/não frequentou, respectivamente). Em cada célula, temos as contagens de indivíduos que pertencem às respectivas categorias das variáveis cruzadas (a, b, c, d) :
Figura 3: Tabela de contingência (tabela 2x2) de exemplo.
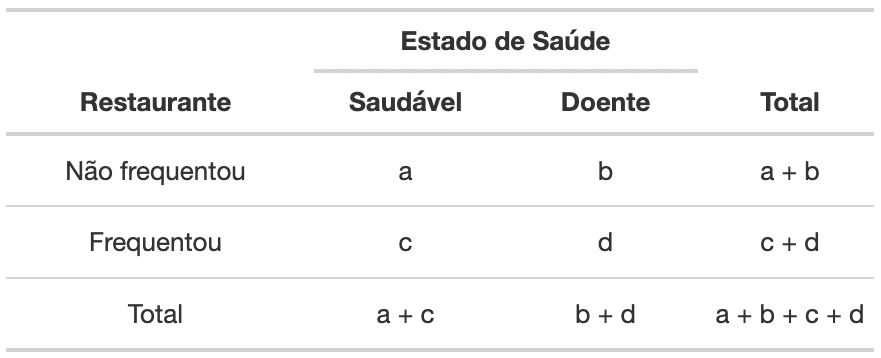
Convencionalmente, as colunas da tabela 2x2 representam a presença ou ausência de um evento ou doença e as linhas a presença ou ausência de exposição a este evento. Da seguinte forma:
- A célula “a” representa os indivíduos que permaneceram saudáveis e não frequentaram o restaurante suspeito.
- A célula “b” representa indivíduos que adoeceram e não frequentaram o restaurante suspeito.
- A célula “c” representa os indivíduos saudáveis e que frequentaram o restaurante suspeito.
- A célula “d” representa os indivíduos que adoeceram e frequentaram o restaurante suspeito.
- Nas marginais da tabela, há os totais, somando linhas e colunas.
Agora, vamos acompanhar algumas análises em que as tabelas 2x2 serão úteis na rotina de trabalho da vigilância em saúde. Vamos lá!
4.1 Associações entre variáveis (Teste qui-quadrado)
Algumas vezes, durante a rotina de análise, precisamos saber se a frequência de uma determinada variável muda quando outra variável está presente e, assim, saber se alguma evidência de associação entre elas ou seria somente uma relação ao acaso. Para isso, podemos utilizar a tabela de contingência (tabela 2x2) e o teste estatístico qui-quadrado.
Definimos a existência de uma associação quando a probabilidade de ocorrência de um evento ou doença se altera quando alguma característica ou outro evento está presente.
Isto acontece com frequência na vigilância, quando estudamos a ocorrência de doença em determinados locais ou testamos hipóteses a partir da investigação de um surto. Dessa forma, estudamos se há possível associação entre uma exposição (fator de risco) e um efeito (doença).
Vamos lá, agora é hora de praticar com exemplos!
Considere que o profissional de vigilância em saúde necessita verificar se a classificação final de dengue no Estado de Rosas possui associação com alguma característica regional como, por exemplo, o local onde o paciente mora. Ou seja, o profissional deve investigar se a frequência de casos prováveis de dengue é diferente entre os municípios de residência dos casos.
Essa investigação é oportuna quando há suspeita de que municípios localizados mais próximos à Capital, por exemplo, poderiam ter mais acesso a estruturas melhores de saúde. Por outro lado, municípios localizados muito distantes das regiões centrais, podem apresentar desigualdades que impactam em muitos aspectos da saúde púbica, inclusive, nas ações contra à dengue. Perceba que essa mesma comparação poderia ser facilmente feita intramunicipal, verificando a diferença entre bairros mais próximos e mais afastados do centro.
Para investigar essa situação, vamos utilizar o agravo dengue da base de notificação do Estado de Rosas. Acompanhe o passo a passo a seguir:
Utilize o banco de dados {
NINDINET.dbf} importado anteriormente;Filtre os registre para os casos notificados de Dengue;
Categorize o município de residência (
ID_MN_RESI) considerando o seguinte:- Registros de casos que residem no município Prímula do Estado de Rosas (código 610213) serão categorizados como da região da “Capital”;
- Registros de casos que residem nos demais municípios do Estado de
Rosas serão categorizados como da região do “Interior”.
Categorize a classificação final de dengue (
CLASSI_FIN) da seguinte forma:- Registros de casos notificados como “1”, “2”, “3”, “4” e “8”, serão categorizados como “Caso provável”;
- Registros de casos notificados como “5”, serão categorizados como “Caso descartado”.
Acompanhe e replique o script abaixo em seu
RStudio, que demonstra as etapas de 1 a 4, indicadas
anteriormente:
# Criando um novo dataframe com a tabela {`Dados`}
dados_classificados <- dados |>
# Filtrando os agravos de dengue (código "A90") com a função filter()
filter(ID_AGRAVO == "A90") |>
# Criando novas colunas com a função mutate()
mutate(
# Classificando o município de residência do paciente em Prímula (código 610213)
# como "Capital" e os demais como "Interior" com uso da função if_else().
# Ou seja, se o município for igual a 610213 será classificado como Capital e,
# se não, será
# classificado como Interior. Caso houver registros em branco (NA),
#estes continuarão como (NA)
regiao = if_else(ID_MN_RESI == "610213", "Capital", "Interior", NA_character_),
# Classificando os casos em diagnósticos de "casos prováveis" e "descartado"
# com a função case_when()
classificacao = case_when(
CLASSI_FIN %in% c("1", "2", "3", "4", "8") ~ "Casos prováveis",
CLASSI_FIN == "5" ~ "Casos descartados",
TRUE ~ NA_character_
)
) No quinto passo, vamos cruzar os dados em que realizamos a classificação da região de residência e do diagnóstico de dengue utilizando a função
tbl_cross()do pacotegtsummary. Para isso, Iremos utilizar os seguintes argumentos:row: indicação de uma variável categórica na linha;col: indicação de uma variável categórica na coluna;percent: definição se a porcentagem será calculada por colunas ou linhas (column ou row);missing: definição se os valores em branco serão incluídos na tabela.
Agora veja como o passo 5 pode ser escrito em um script
abaixo e replique em seu RStudio:
# Criando uma tabela no formato do pacote gtsummary com o nome tabela
tabela_resid_diag_dengue <- dados_classificados |>
# Criando uma tabela de resumo do cruzamento de informações sobre região e tipo
# de diagnóstico
tbl_cross(
row = regiao,
col = classificacao,
percent = "row",
missing = "no"
)Agora, vamos visualizar a tabela criada, para isso digite apenas seu
nome {tabela_resid_diag_dengue} e clique no botão
“Run”. Fique atento pois a tabela será mostrada no painel
Viewer do RStudio e não no Painel
Console!
Vamos lá, acompanhe o script, replique no seu
RStudio:
# visualizando a tabela "tabela"
tabela_resid_diag_dengue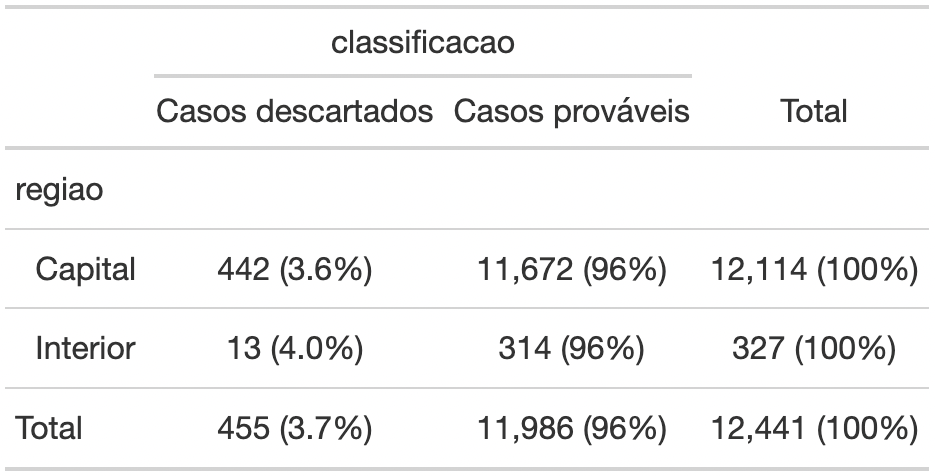
Atenção
Você pode ter observado que o R emiteu um aviso
informando que as observações em branco não foram incluídas na análise.
Este tipo de alerta é muito importante para nos apoiar na interpretação
do que está sendo analisado.
Atente-se sempre às mensagens no output do
R!
Observe que tanto a região da Capital quanto o do Interior do Estado de Rosas possuem porcentagens semelhantes de casos prováveis e de casos descartados. Avaliando a última linha da tabela gerada no output do código, perceberemos que independente da região, 96% dos casos notificados são casos prováveis.
Podemos pensar que, se as variáveis cruzadas não fossem relacionadas, observaríamos as porcentagens muito próximas em cada região. Isso de fato acontece! Portanto, parece não haver associação entre elas. Veja como é importante este relacionamento.
Agora, vamos explorar a presença de significância estatística aplicando o teste qui-quadrado.
Para construir o teste qui-quadrado precisamos admitir:
A hipótese de que a região de residência não tem associação com a classificação final do caso (nesse caso será nossa hipótese nula, como é chamada em estatística, e será a hipótese que vamos testar).
A hipótese de que as variáveis possuem alguma associação será definida como alternativa;
Vamos definir que o nível de significância estatística deve ser menor que 0,05 para rejeitarmos a hipótese nula, ou seja, de que não existe associação da região de residência com a classificação final.
Pronto, agora vamos realizar o teste qui-quadrado para verificar se
esta associação é somente devido ao acaso. Podemos fazer isso através da
função add_p() do pacote gtsummary. Ao
adicionarmos esta função, as células da tabela são verificadas e o teste
estatístico adequado é realizado.
Acompanhe o script abaixo e digite estes comandos em seu
RStudio:
# Adicionado o teste estatítico com a função add_p()
tabela_resid_diag_dengue |> add_p()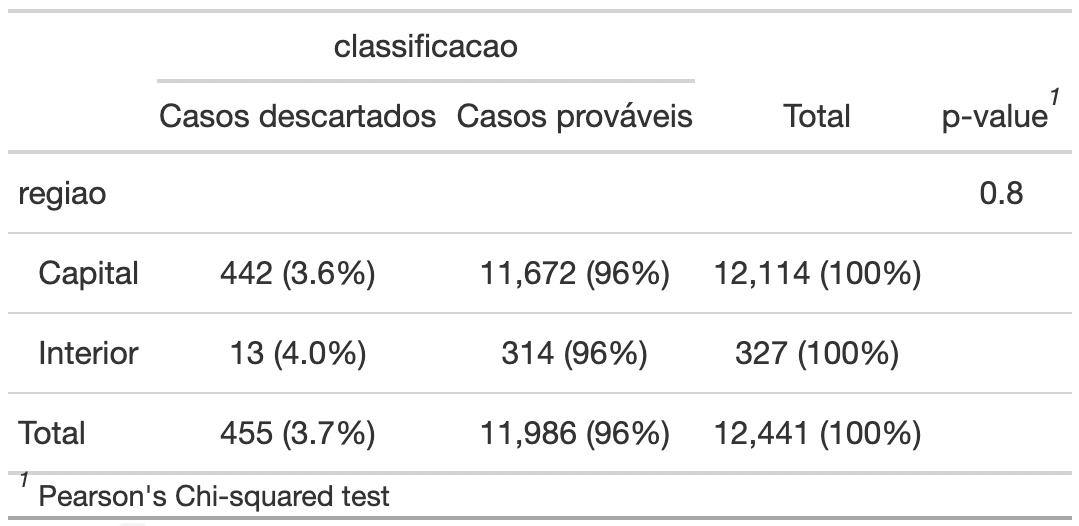
Observe que o resultado do valor do p foi 0,8. O que
isso significa? Como 0,8 é maior que 0,05, não podemos rejeitar a
hipótese nula que definimos anteriormente. Assim, temos
evidência que não há associação entre a região de residência e a
classificação final de Dengue.
Interessante, não é mesmo? Isso faz sentido, pois a dengue está muito espalhada pelo território, sem distinção de local de residência. O mosquito Aedes aegypti não reconhece as barreiras ou fronteiras geográficas.
O teste qui-quadrado \(\chi^2\) também pode ser executado
utilizando a função chisq.test(), nativa da linguagem
R. O argumento essencial dessa função é um
dataframe contendo os dados da tabela 2x2. Observe o
script abaixo, no qual criamos o dataframe e usamos o
pipe (|>) para executarmos diretamente a função
chisq.test.
A tabela foi montada conforme o script abaixo. Digite os
comandos a seguir em seu RStudio:
#Inserindo os dados para construir a tabela (dataframe)
#2x2
#Capital = c(casos prováveis, casos descartados),
#Interior = c(casos prováveis, casos descartados)
data.frame(Capital = c(11672, 442),
Interior = c(314, 13)) |>
#calculando agora o teste qui-quadrado
chisq.test()#>
#> Pearson's Chi-squared test with Yates' continuity
correction
#>
#> data: data.frame(Capital = c(11672, 442),
Interior = c(314, 13))
#> X-squared = 0.026064, df = 1, p-value = 0.8717Percebeu que o valor do p é bem próximo? O pacote
gtsummary utliza essa mesma função para realizar os
cálculos. Escolha o que achar mais fácil de usar.
Atenção
O teste qui-quadrado possui limitações nos cálculos quando o total de pessoas a serem avaliadas é pequeno.
Não há uma definição clara do número, mas valores menores que 30 pessoas ou células da tabela 2x2 com menos de 5 observações são indicativos que um teste estatístico mais apropriado deve ser escolhido, por exemplo, o teste exato de Fisher.
Vamos praticar! Imagine agora que temos apenas 3 casos prováveis na
Capital e 2 descartados, e no Interior 2 casos prováveis e 3
descartados, criaremos um data.frame com a estrutura de tabela 2x2
usando a função fisher.test() do R. Iremos
considerar as seguintes hipoteses:
𝐻o: proporção de casos prováveis na “Capital” é
igual a proporção de casos prováveis na “Interior”.
𝐻1: proporção de casos prováveis na “Capital” é
maior que a proporção de casos prováveis na “Interior”.
Acompanhe o script abaixo e reproduza em seu
RStudio:
# Inserindo os dados para construir a tabela (dataframe)
# 2x2
data.frame(Capital = c(3, 2),
Interior = c(2, 3)) |>
# O teste exato de Fisher é feito usando a função
# `fisher.test()`
fisher.test(dataframe,
# argumento `alternative`indica a hipótese
# alternativa do teste
alternative = "greater",
# argumento `conf.int` indica que o
# intervalo de confiança deve ser construído
conf.int = TRUE,
# argumento `conf.level` indica o nível de
# confiança a ser utilizado para a
# construção do intervalo
conf.level= 0.95
)#>
#> Fisher's Exact Test for Count Data
#>
#> data: data.frame(Capital = c(3, 2),
Interior = c(2, 3))
#> p-value = 0.5
#> alternative hypothesis: true odds ratio is greater
than 1
#> 95 percent confidence interval:
#> 0.1541449 Inf
#> sample estimates:
#> odds ratio
#> 2.069959Observe que no output serão apresentados o seguintes retornos:
- p-valor do teste,
- a hipótese alternativa em consideração,
- o intervalo de confiança construído baseado na hipótese alternativa, e
- a estimativa da razão de chances com base na tabela de contingência.
Com o teste podemos concluir que não há evidências para rejeitar Ho (p=0,50), ou seja, não há evidências de que na Capital os casos prováveis é maior que o número de casos provavéis no população do Interior.
Para o aprofundamento no tema, livros de bioestatística devem ser consultados.


