Você se lembra do mapa de papel com alfinetes representando casos espalhados pelo município? Ele também é um exemplo de representação espacial. A representação espacial de evento de saúde é o processo de criar símbolos que representem as ruas, os bairros ou os casos acometidos por alguma doença e possam ser interpretados pelas pessoas. Os mapas são extremamente úteis e bem difundidos para esta tarefa.

Mas, o que seria um mapa? Mapa é um meio de comunicação gráfica, visual ou até tátil que representa algum fenômeno do mundo real. Tudo o que acontece na superfície terrestre pode ser espacializado e representado. O produto da transformação do dado espacial coletado, processado, editado e integrado em uma visualização com nível de detalhe específico é um mapa.

No R, a criação de mapas pode utilizar vários pacotes. Vamos praticar com os principais, como o pacote sf, e outros que tenham maior simplicidade para manejo, como os pacotes mapsf e tmap. Mas não se preocupe, falaremos deles mais à frente. Neste momento, precisaremos instalá-los e carregá-los. Execute o código abaixo no seu computador:

# Instalando e carregando os pacotes necessários

if(!require(tidyverse)) install.packages("tidyverse");library(tidyverse)
if(!require(foreign)) install.packages("foreign");library(foreign)
if(!require(readxl)) install.packages("readxl");library(readxl)
if(!require(janitor)) install.packages("janitor");library(janitor)
if(!require(stringi)) install.packages("stringi");library(stringi)
if(!require(sf)) install.packages("sf");library(sf)
if(!require(mapsf)) install.packages("mapsf");library(mapsf)
if(!require(tmap)) install.packages("tmap");library(tmap)
if(!require(ggspatial)) install.packages("ggspatial");library(ggspatial)

Agora vamos conhecer os elementos básicos que compõem um mapa, como importar arquivos vetoriais e visualizá-los como um mapa no R. Acompanhe com atenção os próximos tópicos.

O mapa é uma simplificação da realidade. Por isso, precisamos priorizar qual nível de detalhe expressa melhor a realidade que queremos representar. Esta tarefa não é trivial. É necessário o conhecimento de conceitos importantes para a melhor representação possível de um fenômeno. Um mapa errado pode levar a interpretações e decisões equivocadas, gasto irracional de dinheiro público.

Alguns elementos devem fazer parte na elaboração de mapas. Esses elementos são focados na comunicação com o leitor, por meio de informações elementares na representação dos fenômenos. De modo geral, podem ser elementos de comunicação que visam melhor explicar o que está sendo mapeado, apresentando informações sobre o assunto, mas também podem ser elementos cartográficos, para explicar as referências cartográficas utilizadas para sobre a elaboração do mapa. Os principais elementos são:

• Título: elemento de comunicação que deve mostrar o assunto, onde e quando o fenômeno representado aconteceu. A depender das regras de elaboração utilizadas para a montagem do mapa ou relatório que o mapa seja incluído (como por exemplo, normas da Associação Brasileira de Normas Técnicas - ABNT, de periódicos científicos ou regras de publicação definidas pelo setor de comunicação) pode conter tamanho de letra e posição específicas;

• Legenda: elemento de comunicação de decodificação dos símbolos, relações, cores, formas e texturas utilizadas no mapa, sendo considerado um guia para a leitura. Mais adiante no material serão discutidas formas de classificação a depender do tipo de mapa produzido;

• Escala: elemento cartográfico que representa a relação entre o tamanho dos elementos representados em um mapa e o tamanho real. Na área da saúde, geralmente, é representada em sua forma gráfica, por uma linha ou barra subdivida em trechos nos quais cada comprimento significa o valor correspondente na superfície;

• Seta norte: elemento de orientação na superfície terrestre oriundo dos pontos cardeais;

• Fonte dos dados: descrição da origem dos dados utilizados para a elaboração e digitalização do mapa. A depender das normas de elaboração utilizadas, podem ser apenas citados na seção de métodos de relatórios, por exemplo;

• Sistema Geodésico de Referência: é um conjunto de parâmetros para ajustar a forma real da Terra à geometria que melhor representa. Existem diversos sistemas geodésicos que se ajustam melhor de acordo com a região do mundo. No Brasil, desde 2015 o Sistema de Referência Geocêntrico para as Américas (SIRGAS2000) foi definido como padrão.

  O sistema de coordenadas é um dos elementos do sistema geodésico. É por meio dele que é possível localizar algo na superfície terrestre. De modo geral, esse posicionamento pode ser feito por meio de dois sistemas:

  • O sistema de coordenadas geográficas, que utiliza linhas verticais (meridianos) e linhas horizontais (paralelos) posicionadas no globo para definir a localização espacial de um objeto. Essa localização é, então, especificada em graus decimais (ou em graus, minutos e segundos) por meio da longitude e da latitude.

  • O sistema de coordenadas planas, que utiliza uma projeção em plano no qual uma localização é representada por X e Y, especificada em metros. A projeção mais utilizada na saúde pública é a do sistema Universal Transverso de Mercator (UTM), que utiliza a divisão da Terra em fusos. Com ela, é possível aplicar funções de cálculos de distâncias entre pontos e comprimento de linhas mais facilmente.

Atenção

Quando lidamos com diferentes dados, os sistemas de referência podem ser diferentes. Usar referências diferentes resultará em locais em posições diferentes ou arquivos que não se sobrepõem corretamente, ou seja, não são representados adequadamente.

Logo, é uma boa prática utilizar o mesmo sistema de referência em todos os projetos e arquivos geográficos em que se estiver trabalhando.

No R, as coordenadas de ambos os sistemas citados estão indexadas pelo código EPSG (sigla em inglês para European Petroleum Survey Group que, em português, pode ser traduzido para Grupo Europeu de Pesquisa de Petróleo). Nesta indexação, o sistema geográfico adotado pelo Brasil, o SIRGAS2000, possui o código 4674. 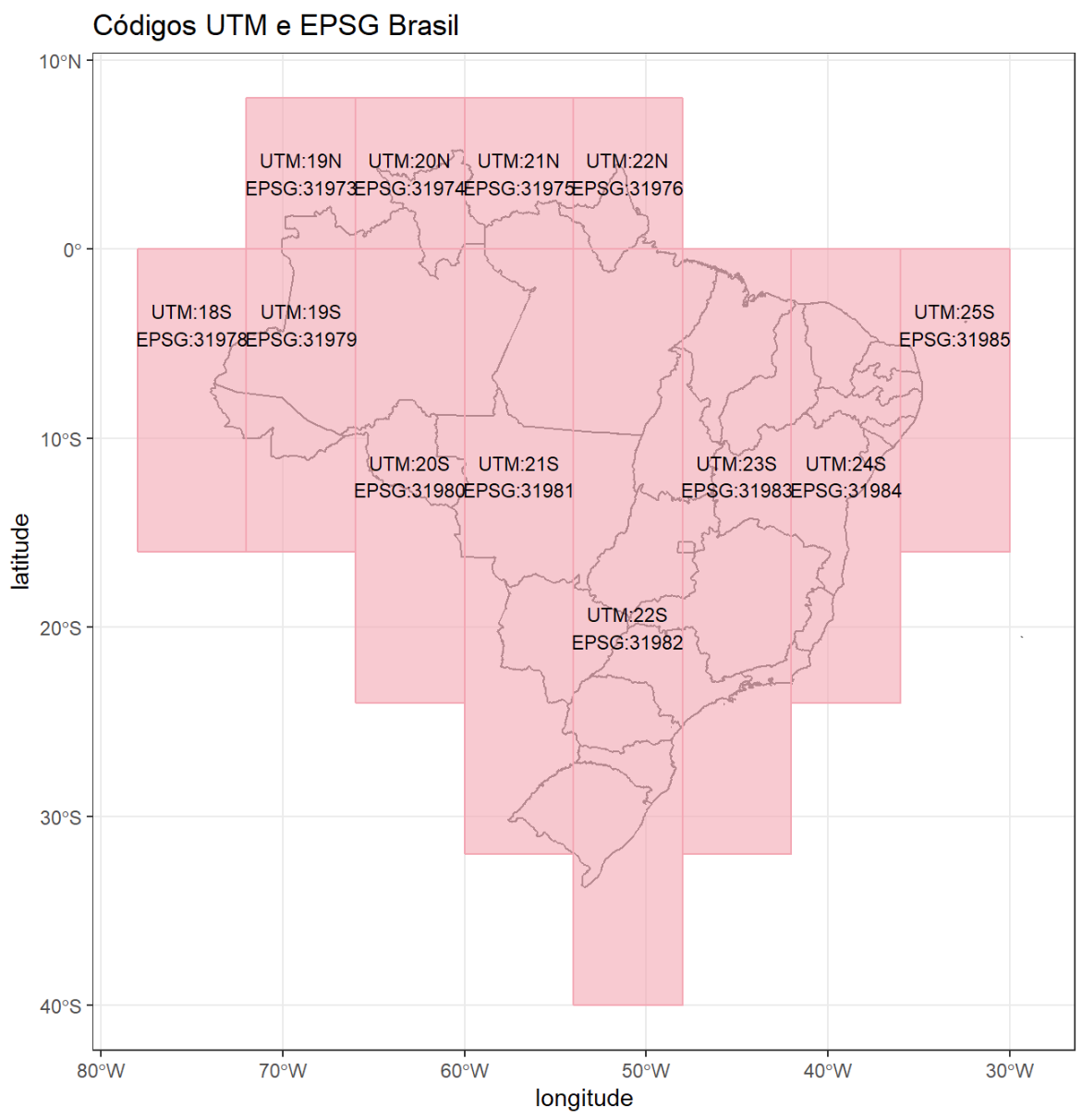Para o sistema de coordenadas planas UTM há vários códigos, de modo que cada região coberta por um fuso possui um código (Figura 2).

É comum um município adotar um sistema de coordenada como padrão, mas acontece de alguns estarem em áreas limites entre dois fusos. Nesta situação, para elaboração de mapas, é sugerido a adoção de um sistema de coordenadas que utiliza projeção cônica cujo código EPSG é 5880.

As cores despertam respostas emocionais diferentes nas pessoas, a depender do contexto. Por exemplo, ao elaborar um mapa com área de risco para determinada doença, utilizar a cor azul pode passar uma sensação de tranquilidade, além de poder confundir o leitor, fazendo-o pensar em ser uma representação de um rio ou lago. Então a questão é: como escolher as cores adequadamente?

Ao elaborar mapas, o profissional da Vigilância em Saúde deve ter em mente sobre o que cabe destacar no mapa e como a cor contribui com o seu objetivo. Não é uma questão de gosto, mas uma forma de comunicação que utiliza um simbolismo psicológico que pode ser muito eficiente se bem utilizada. A depender do tipo de variável que se deseja utilizar para representação no mapa, o grupo de cores devem ser apropriadas.

Existem muitas maneiras de especificar as cores no R. Uma das formas mais usadas é o padrão RGB (do inglês: “Red, Green, Blue”), que representa a intensidade das cores primárias vermelho, verde e azul. Uma das codificações desse padrão é o formato chamado hexadecimal, formado por seis dígitos, dois para cada cor primária. Esses dois dígitos podem ser representados por números que variam de 00 a 99 e pares de letras de AA até FF (por exemplo AB, AC, CE, EF, FF).

R = 00 a 99 / AA a FF
G = 00 a 99 / AA a FF
B = 00 a 99 / AA a FF

No R, o símbolo (#) nesta situação indica que é um código hexadecimal. Então, um código #000000 representa a cor preta e #FFFFFF representa a cor branca. Combinando as três cores básicas podemos especificar mais de 16 milhões de cores e tons de cinza!

Uma pequena amostra de cores pode ser vista na tabela abaixo, mas é possível visualizar as combinações possíveis clicando em https://www.w3schools.com/colors/colors_hexadecimal.asp. Na tabela, mostramos a cor em cada célula e, também, o código hexadecimal.

Para a representação de indicadores que expressam valores relativos (razão, taxas), deve-se seguir a lógica de ordenação (menor para maior, maior que, menor que). A escolha mais adequada é representá-los por meio de variação de cores, utilizando paletas de cores mais adequadas e intuitivas:

• sequenciais: são paletas de gradientes que, de modo geral, denotam que cores mais claras representam valores baixos e cores mais escuras representam valores altos. Podem também representar uma gradação de uma única cor, por exemplo do verde claro para o verde escuro (neste caso é chamada matiz única), ou utilizar gradação de cores diferentes, por exemplo do amarelo para o roxo (sendo chamada matiz múltipla). São muito intuitivas na representação de mapas temáticos e muito comuns de escolha em produtos gráficos na Vigilância em Saúde.

• divergentes: também são gradientes, mas possuem um ponto médio mais claro entre duas extremidades escuras destacadas. São usadas para representar variáveis com valores que transitam de um extremo para outro e, principalmente, quando a variável a ser representada possui um valor “central” como, por exemplo:

  • zero: taxas de crescimentos que variam de valores negativos a positivos, passando pelo zero;
  • porcentagens e proporções: valores que variam de 0 a 1 (ou 0% a 100%);
  • meta: indicadores que possuem uma pactuação, uma meta a ser atingida;
  • média ou mediana: taxas que apresentem médias gerais ou medianas.

Ambas as paletas podem representar uma gradação de cores contínua (também chamada de não categorizada) e discretizada (também chamada de classificada, escalonada, graduada). Na tabela abaixo, apresentamos alguns exemplos:

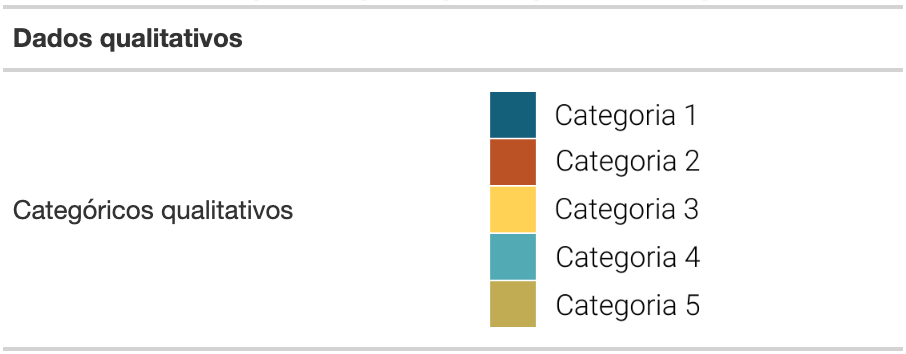
As paletas de cores voltadas para dados categóricos representam uma cor associada a cada categoria de uma variável que não pode ser ordenada ou representam dados qualitativos que não podem ser mensurados (somados ou calculados em média). Neste caso, a escolha de cor privilegia a diferenciação clara entre as categorias.

No menu lateral “Arquivos” do curso se encontra um arquivo em PDF com as cores e nomes nativas da linguagem R. Há vários pacotes que ampliam as opções de cores como RColorBrewer e colorspace.

Lembramos há pouco dos mapas com alfinetes utilizados para representação de eventos. Atualmente, a representação é muito mais focada no meio digital. Mapas digitais são aqueles desenvolvidos utilizando um conjunto de ferramentas, incluindo programas de computador, editados e disponibilizados em formato digital em páginas online ou em relatórios enviados por email, por exemplo.

A representação dos objetos geográficos no meio digital é feita por dados do tipo gráfico. Esses dados são assim chamados porque utilizam um conjunto de geometrias para descrever, graficamente, os objetos geográficos que compõem os arquivos vetoriais. Três tipos básicos de geometria são utilizados: pontos, linhas e polígonos.

A importação de arquivos vetoriais no R pode ser feita utilizando o pacote sf (referente às palavras em inglês simple feature). O pacote sf importa e lê esses arquivos como dataframes, sendo as geometrias armazenadas em colunas. Dessa forma, podem ser normalmente manipuladas com pacotes como o dplyr e ter visualizações com pacotes como o ggplot2.

Vamos conhecer um pouco mais das principais geometrias e, para isso, considere que foi solicitado pelo diretor geral, um mapa contendo as localizações das unidades de saúde e as ruas de acesso até estas unidades. Considere também utilizar dados do Estado do Acre para executar esta tarefa. Acompanhe com atenção os conceitos que seguem.

a) Pontos

Vamos importar dados de pontos contendo a localização das unidades de saúde do Estado do Acre. A geometria de pontos é composta por um conjunto de pares de coordenadas que representam a posição de um evento, estrutura física ou um objeto geográfico qualquer no espaço. Em geral, são usados para indicar um local específico.

Na nossa tarefa, vamos utilizar a função read_sf() do pacote sf para importar os dados de coordenadas das unidades de saúde {ac_unidades}, disponível no menu lateral “Arquivos” do curso, juntamente com os arquivos auxiliares. Importante baixar todos na mesma pasta.

A função read_sf() possui como argumento obrigatório apenas o arquivo a ser importado. Como veremos mais à frente, essa função é genérica, pois pode ser usada para importar qualquer geometria (pontos, linhas, polígonos). Agora é com você. Execute o comando abaixo no seu RStudio. Lembre-se que os pacotes já devem estar instalados e carregados.

# Importando dados vetoriais de pontos com a função read_sf() e
# salvando no objeto `ac_unidades`
ac_unidades <- read_sf('Dados/ac_unidades_saude_m.shp')

Vamos aproveitar esta importação para analisar a estrutura do arquivo. Digite o nome do objeto salvo (ac_unidades) no Painel Console e veja o output:

# Analisando o arquivo importado
ac_unidades

#> Simple feature collection with 1008 features and 4 fields
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: -73.22469 ymin: -11.029 xmax: -66.64395 ymax: -7.417815
#> Geodetic CRS:  SIRGAS 2000
#> # A tibble: 1,008 × 5
#>    uf    code_state cod_mun cnes_n               geometry
#>    <chr>      <dbl>   <dbl> <chr>             <POINT [°]>
#>  1 AC            12  120035 3591018 (-72.68529 -9.309803)
#>  2 AC            12  120001 3638685      (-66.883 -9.828)
#>  3 AC            12  120001 7245890      (-66.883 -9.828)
#>  4 AC            12  120001 7026641 (-67.05353 -10.07714)
#>  5 AC            12  120001 0257184      (-66.883 -9.828)
#>  6 AC            12  120001 3382745      (-66.883 -9.828)
#>  7 AC            12  120001 3006166      (-66.883 -9.828)
#>  8 AC            12  120001 9639896      (-66.883 -9.828)
#>  9 AC            12  120001 3393984      (-66.883 -9.828)
#> 10 AC            12  120001 0153281      (-66.883 -9.828)
#> # … with 998 more rows
#> # ℹ Use `print(n = ...)` to see more rows

Um sumário parecido com o apresentado acima deve ser mostrado no seu RStudio. O output contém os seguintes elementos:

1. a quantidade de registros e atributos (número de linhas e colunas);
2. o tipo de geometria;
3. os limites geográficos dos dados (também chamado de bounding box );
4. o sistema de referência (sigla CRS);
5. o objeto geográfico em si (sf - simple feature);
6. a coluna do tipo lista contendo a geometria (objeto de classe sfc - sigla para simple feature column);
7. a geometria individual referente ao objeto geográfico identificado pelo item 5 (objeto de classe sfg - sigla para simple feature geometry).

Reveja os elementos descritos acima identificados na Figura 3:

Bem fácil, não é mesmo? Importamos 1008 unidades de saúde, entre postos de saúde, consultórios e hospitais. Vamos agora, importar os demais dados para executar a nossa tarefa.

O formato de arquivo mais utilizado para armazenar dados espaciais é o shapefile. Este arquivo é formado por três arquivos básicos que armazenam informações diferentes e devem, obrigatoriamente, permanecerem na mesma pasta:

• “.shp”: arquivo com os dados da geometria em si;
• “.shx”: arquivo de índice posicional;
• “.dbf”: arquivo de atributos das formas representadas pelo shp.

Eventualmente, também compõem o conjunto de arquivos shapefile:

• “.prj”: arquivo de texto que contém a projeção dos dados;
• “.sbn” e “.sbx”: índice espacial;
• “.shp.xml”: metadados.

Mais recentemente, e devido às limitações do shapefile, o uso de arquivo no formato geopackage têm aumentado. Diferente do shapefile, esse formato, cuja extensão é “.gpkg”, é um arquivo único, comporta várias camadas de geometrias diferentes e suporta tamanhos maiores de bases.

Também os arquivos KML, sigla que se refere a Keyhole Markup Language, têm sido muito utilizados no ambiente das secretarias de saúde. Esse arquivo possui um formato para visualização espacial em aplicativos como Google Earth e Google Maps.

Esses arquivos e muitos outros formatos podem ser lidos no R e, inclusive, utilizando a mesma função do pacote sf, que será apresentada no próximo tópico.

Para saber mais sobre os tipos de arquivos vetoriais que são aceitos pelo pacote, clique aqui.

b) Linhas

Vamos importar um arquivo vetorial de linhas, {ac_vias}, que representam as ruas e rodovias do Estado do Acre, disponível no menu lateral “Arquivos” do curso, juntamente com os arquivos auxiliares. Importante baixar todos na mesma pasta.

Os dados vetoriais de linhas são conceituados como conjuntos de pares de coordenadas conectados, com início e fim definido. As linhas são usadas para representar objetos geográficos que denotam algum comprimento como estradas ou ruas, por exemplo. Também é utilizada em análises para representar distâncias entre pontos, tendência de deslocamentos, entre outros.

Vamos lá, novamente, utilize a função read_sf para importar o arquivo {ac_vias}. Execute o código abaixo no seu computador.

# Importando dados vetoriais de linhas com a função read_sf() e
# salvando no objeto `ac_vias`
ac_vias <- read_sf('Dados/ac_vias.shp')

# Analisando o arquivo importado
ac_vias

#> Simple feature collection with 18423 features and 14 fields
#> Geometry type: MULTILINESTRING
#> Dimension:     XY
#> Bounding box:  xmin: -73.74049 ymin: -11.1454 xmax: -66.6359 ymax: -7.135078
#> Geodetic CRS:  SIRGAS 2000
#> # A tibble: 18,423 × 15
#>      fid osm_id     code fclass   name  ref   oneway maxsp…¹ layer bridge tunnel
#>    <dbl> <chr>     <dbl> <chr>    <chr> <chr> <chr>    <dbl> <dbl> <chr>  <chr> 
#>  1 45637 379159318  5122 residen… Rua … <NA>  B            0     0 F      F     
#>  2 45632 379159312  5122 residen… Rua … <NA>  B            0     0 F      F     
#>  3 45635 379159315  5122 residen… <NA>  <NA>  B            0     0 F      F     
#>  4 45618 379159294  5122 residen… Rua … <NA>  B            0     0 F      F     
#>  5 45639 685642583  5122 residen… <NA>  <NA>  B            0     0 F      F     
#>  6 45621 379159297  5122 residen… Rua … <NA>  B            0     0 F      F     
#>  7 45623 379159299  5122 residen… Rua … <NA>  B            0     0 F      F     
#>  8 45625 379159302  5122 residen… Rua … <NA>  B            0     0 F      F     
#>  9 45612 379159287  5122 residen… Rua … <NA>  B            0     0 F      F     
#> 10 45613 379159288  5122 residen… Rua … <NA>  B            0     0 F      F     
#> # … with 18,413 more rows, 4 more variables: NM_MUN <chr>, SIGLA_UF <chr>,
#> #   cod_mun <chr>, geometry <MULTILINESTRING [°]>, and abbreviated variable
#> #   name ¹​maxspeed
#> # ℹ Use `print(n = ...)` to see more rows, and `colnames()` to see all variable 
names

Podemos perceber que importamos 18423 linhas entre rodovia e ruas. Mais à frente, veremos como podemos visualizar esses dados, inclusive, sobrepondo com os demais dados importados.

Você percebeu que este arquivo vetorial de linhas possui algumas ruas sem nome? Inclusive, algumas ruas que existem podem não estar sendo representadas. Isso é comum na realidade e deve ser uma limitação a ser superada, buscando arquivos mais atualizados. Parcerias com setor de geoprocessamento do município são úteis para acesso a dados mais atuais ou com menos imperfeições.

c) Polígonos

Para finalizar a importação dos dados para executar nossa tarefa, vamos importar os limites administrativos dos municípios do Acre presentes no arquivo {ac_municipios}, disponível no menu lateral “Arquivos” do curso, juntamente com os arquivos auxiliares. Importante baixar todos na mesma pasta. Esses limites utilizam a geometria de um polígono para serem representados.

Polígonos são conjuntos de linhas que possuem, em geral, o mesmo ponto de início e fim, denotando uma estrutura fechada. Representam áreas, territórios, ou uma determinada região de destaque qualquer (por exemplo áreas de risco para alguma doença) ou com características similares (regiões climáticas, biomas).

Utilizando a função read_sf, importe o arquivo {ac_municipios} seguindo o código abaixo.

# Importando dados vetoriais de polígonos com a função read_sf() e
# salvando no objeto `ac_municipios` 
ac_municipios <- read_sf('Dados/ac_municipios.shp')

# Analisando o arquivo importado
ac_municipios

#> Simple feature collection with 22 features and 5 fields
#> Geometry type: POLYGON
#> Dimension:     XY
#> Bounding box:  xmin: -73.99045 ymin: -11.14556 xmax: -66.62368 ymax: -7.111824
#> Geodetic CRS:  SIRGAS 2000
#> # A tibble: 22 × 6
#>    CD_MUN  NM_MUN          SIGLA AREA_KM2 cod_mun                       geometry
#>    <chr>   <chr>           <chr>    <dbl> <chr>                    <POLYGON [°]>
#>  1 1200013 Acrelândia      AC       1812. 120001  ((-67.13181 -9.677307, -66.62…
#>  2 1200054 Assis Brasil    AC       4979. 120005  ((-69.59034 -10.3717, -69.586…
#>  3 1200104 Brasiléia       AC       3928. 120010  ((-69.12866 -10.39925, -69.12…
#>  4 1200138 Bujari          AC       3035. 120013  ((-68.2199 -9.242753, -67.976…
#>  5 1200179 Capixaba        AC       1706. 120017  ((-67.80225 -10.19873, -67.80…
#>  6 1200203 Cruzeiro do Sul AC       8783. 120020  ((-72.62078 -7.538954, -72.58…
#>  7 1200252 Epitaciolândia  AC       1653. 120025  ((-68.6448 -10.61638, -68.643…
#>  8 1200302 Feijó           AC      27977. 120030  ((-70.05145 -7.84816, -69.444…
#>  9 1200328 Jordão          AC       5357. 120032  ((-71.56361 -8.64941, -71.560…
#> 10 1200336 Mâncio Lima     AC       5452. 120033  ((-73.1655 -7.341657, -72.900…
#> # … with 12 more rows
#> # ℹ Use `print(n = ...)` to see more rows

Analisando o arquivo importado, percebemos que os 22 municípios do Acre foram importados. Agora, vamos conhecer as principais funções para visualizar os dados espaciais que importamos.

A visualização de dados espaciais é uma atividade muito comum e, às vezes, confundida com a análise espacial. Isso ocorre porque, com um bom produto de visualização, é possível realizar análises que compõem, de fato, uma análise de dados.

Algumas funções do pacote sf emitem outputs similares como os citados acima como, por exemplo a função st_geometry(), que tem como argumento principal apenas o arquivo vetorial a ser avaliado. Repita as linhas a seguir no seu RStudio e observe o resultado:

# Visualizando informações sobre o objeto ac_municipios 
# com a função st_geometry()
st_geometry(ac_municipios)

#> Geometry set for 22 features
#> Geometry type: POLYGON
#> Dimension: XY
#> Bounding box: xmin: -73.99045 ymin: -11.14556 xmax: -66.62368 ymax: -7.111824
#> Geodetic CRS: SIRGAS 2000
#> First 5 geometries:
#> POLYGON ((-67.13181 -9.677307, -66.62689 -9.898…
#> POLYGON ((-69.59034 -10.3717, -69.58664 -10.371…
#> POLYGON ((-69.12866 -10.39925, -69.12937 -10.40…
#> POLYGON ((-68.2199 -9.242753, -67.97684 -9.3527…
#> POLYGON ((-67.80225 -10.19873, -67.80008 -10.20…

Para concluir nossa tarefa de visualizar as localizações das unidades de saúde e as ruas de acesso até estas unidades, vamos aprofundar um pouco mais na visualização dos dados espaciais, pois vamos precisar entender as principais funções que permitem essa visualização e quais detalhes podem melhorar a qualidade do nosso trabalho.

Para seguir com a criação dos mapas, vamos realizar um procedimento muito comum ao trabalhar com arquivos vetoriais: a transformação do sistema de coordenadas.

A transformação do sistema de coordenadas deve ser realizada quando:

• A região geográfica da análise possui uma extensão relativamente pequena e sistema de referência do arquivo vetorial está como sistema de coordenadas geográficas e não planas,
• A análise envolver vários arquivos vetoriais e que, eventualmente, alguns estão em sistemas de coordenadas diferentes,
• Os pacotes utilizados para mapeamento possuem um melhor desempenho com sistemas de coordenadas planas.

Para regiões geográficas relativamente pequenas (extensão de um município ou um pequeno grupo de municípios), o sistema de coordenadas planas é indicado, sendo o sistema UTM o mais comum, já que esses locais estão inclusos em um único fuso.

Como já vimos anteriormente, quando a região de interesse tem uma extensão muito grande e está localizada entre dois ou mais fusos, é indicada a adoção da projeção policônica cujo código EPSG é 5880 (Projeção Policônica SIRGAS 2000).

Como podemos perceber na Figura 2, o Estado do Acre está localizado entre os fusos 18 e 19 e, dessa forma, indica que vamos precisar transformar o sistema de coordenadas do nosso arquivo vetorial.

Para verificar qual o sistema de coordenadas estão nossos arquivos, vamos utilizar a função st_crs() do pacote sf. Essa função possui como argumento principal o nome do arquivo vetorial. Acompanhe o script abaixo e reproduza-o no seu RStudio:

# Verificando o sistema de coordenadas de referência
st_crs(ac_municipios)

#> Coordinate Reference System:
#>   User input: SIRGAS 2000 
#>   wkt:
#> GEOGCRS["SIRGAS 2000",
#>     DATUM["Sistema de Referencia Geocentrico para las AmericaS 2000",
#>         ELLIPSOID["GRS 1980",6378137,298.257222101,
#>             LENGTHUNIT["metre",1]]],
#>     PRIMEM["Greenwich",0,
#>         ANGLEUNIT["degree",0.0174532925199433]],
#>     CS[ellipsoidal,2],
#>         AXIS["geodetic latitude (Lat)",north,
#>             ORDER[1],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>         AXIS["geodetic longitude (Lon)",east,
#>             ORDER[2],
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>     USAGE[
#>         SCOPE["Horizontal component of 3D system."],
#>         AREA["Latin America - Central America and South America - onshore and 
offshore. Brazil - onshore and offshore."],
#>         BBOX[-59.87,-122.19,32.72,-25.28]],
#>     ID["EPSG",4674]]

Perceba que na primeira linha já é mostrado o sistema de referência e na última linha mostra o código EPSG. O nosso arquivo, portanto, se encontra no sistema de coordenadas geográficas SIRGAS 2000, código 4674.

Para transformar do sistema de coordenadas geográficas, código 4674, para coordenadas planas, código 5880 vamos utilizar a função st_transform() do pacote sf. Os argumentos principais dessa função são:

• x = arquivo vetorial importado pelo pacote sf. Nesse caso, vamos utilizar {ac_municipios};
• crs = sistema de referência de destino. Neste argumento são aceitos códigos EPSG.

Acompanhe o código abaixo e reproduza no computador:

# Transformando o sistema de coordenadas do objeto `ac_municipios` 
# com a função st_transform()
ac_municipios_5880 <- st_transform(x = ac_municipios, crs = 5880)


# Verificando a trasnformação do
# sistema de coordenadas de referência
st_crs(ac_municipios_5880)

#> Coordinate Reference System:
#>   User input: EPSG:5880 
#>   wkt:
#> PROJCRS["SIRGAS 2000 / Brazil Polyconic",
#>     BASEGEOGCRS["SIRGAS 2000",
#>         DATUM["Sistema de Referencia Geocentrico para las AmericaS 2000",
#>             ELLIPSOID["GRS 1980",6378137,298.257222101,
#>                 LENGTHUNIT["metre",1]]],
#>         PRIMEM["Greenwich",0,
#>             ANGLEUNIT["degree",0.0174532925199433]],
#>         ID["EPSG",4674]],
#>     CONVERSION["Brazil Polyconic",
#>         METHOD["American Polyconic",
#>             ID["EPSG",9818]],
#>         PARAMETER["Latitude of natural origin",0,
#>             ANGLEUNIT["degree",0.0174532925199433],
#>             ID["EPSG",8801]],
#>         PARAMETER["Longitude of natural origin",-54,
#>             ANGLEUNIT["degree",0.0174532925199433],
#>             ID["EPSG",8802]],
#>         PARAMETER["False easting",5000000,
#>             LENGTHUNIT["metre",1],
#>             ID["EPSG",8806]],
#>         PARAMETER["False northing",10000000,
#>             LENGTHUNIT["metre",1],
#>             ID["EPSG",8807]]],
#>     CS[Cartesian,2],
#>         AXIS["easting (X)",east,
#>             ORDER[1],
#>             LENGTHUNIT["metre",1]],
#>         AXIS["northing (Y)",north,
#>             ORDER[2],
#>             LENGTHUNIT["metre",1]],
#>     USAGE[
#>         SCOPE["Topographic mapping (small scale)."],
#>         AREA["Brazil - onshore and offshore. Includes Rocas, Fernando de Noronha 
archipelago, Trindade, Ihlas Martim Vaz and Sao Pedro e Sao Paulo."],
#>         BBOX[-35.71,-74.01,7.04,-25.28]],
#>     ID["EPSG",5880]]

Pronto! É um procedimento relativamente simples, não é mesmo? Agora, vamos seguir com a elaboração dos mapas temáticos, abordando primeiramente o mapa base, a primeira camada da nossa sobreposição. Vamos lá?

Vários pacotes no R são úteis para visualizar dados espaciais. Alguns são mais genéricos, tendo a visualização de dados espaciais como um dos itens contemplados na visualização de dados, como é o caso do ggplot2. Outros possuem funções que abordam de forma mais específica a visualização de mapas com temas (mapas temáticos), como é o caso do pacote tmap e mapsf.

Atualmente, um pacote que funciona como uma extensão para o ggplot2 chamado ggspatial auxilia em alguns pontos na padronização da visualização de mapas. Mas, se o objetivo é apenas uma visualização rápida, a função plot(), nativa do R, pode auxiliar bastante. Vamos conhecer alguns deles no próximo tópico.

Agora que já vimos os elementos básicos para um mapa e como utilizar as cores para melhorar a qualidade do nosso produto, vamos iniciar a entender como visualizar os arquivos de dados espaciais.

Vamos iniciar com um arquivo que importamos anteriormente, o {ac_municipios}, disponível no menu lateral “Arquivos” do curso, juntamente com os arquivos auxiliares. Importante baixar todos na mesma pasta.

Esse arquivo contém dados vetoriais de polígonos, os limites dos municípios do Acre. Contudo, na rotina do trabalho da vigilância no nível municipal, pode haver arquivos que representam bairros, localidades de trabalho da equipe de endemias, áreas de abrangência da estratégia de saúde da família, setor censitário, regiões administrativas ou áreas de planejamento. O funcionamento das funções apresentadas é o mesmo.

Com a função plot(), que vamos utilizar agora, o argumento essencial (x) é o objeto a ser visualizado. É possível combinar com a função st_geometry() do pacote sf para visualizar apenas a geometria, sem os outros campos. Faça a plotagem do objeto no seu RStudio com o comando a seguir:

# Plotando e visualizando o objeto `ac_municipios`
plot(x = st_geometry(ac_municipios))

Bem fácil, não é mesmo? Contudo, essa visualização é útil para atender a objetivos que não são necessários elementos de comunicação, como os apresentados no item 3.1. Mas, para melhorar a qualidade do nosso mapa, alguns outros argumentos podem ser utilizados como, por exemplo:

• axes: plota as coordenadas nos eixos x e y;
• graticule: plota uma grade que acompanha as coordenadas;
• col: define a cor de preenchimento (no caso de polígonos);
• xlab e ylab: define os rótulos dos eixos;
• main: apresenta um título centralizado no topo do mapa.

Agora, vamos utilizar estes elementos e criar um mapa mais completo, embora ainda sem todos os elementos. Execute as linhas a seguir em seu RStudio:

# Plotando e visualizando o objeto ac_municipios
plot(
  
  # Definindo o objeto que será utilizado para a visualização do mapa
  x = st_geometry(ac_municipios),
  
  # Definindo como verdadeiro o argumento para plotagem das coordenadas 
  # nos eixos do gráfico
  axes = TRUE,
  
  # Definindo como verdadeiro o argumento para plotagem da grade com as
  # coordenadas
  graticule = TRUE,
  
  # Definindo a cor de preenchimento (código hexadecimal)
  col = "#FAFAFA",
  
  # Definindo os rótulos dos eixos x e y
  xlab = "longitude",
  ylab = "latitude"
)

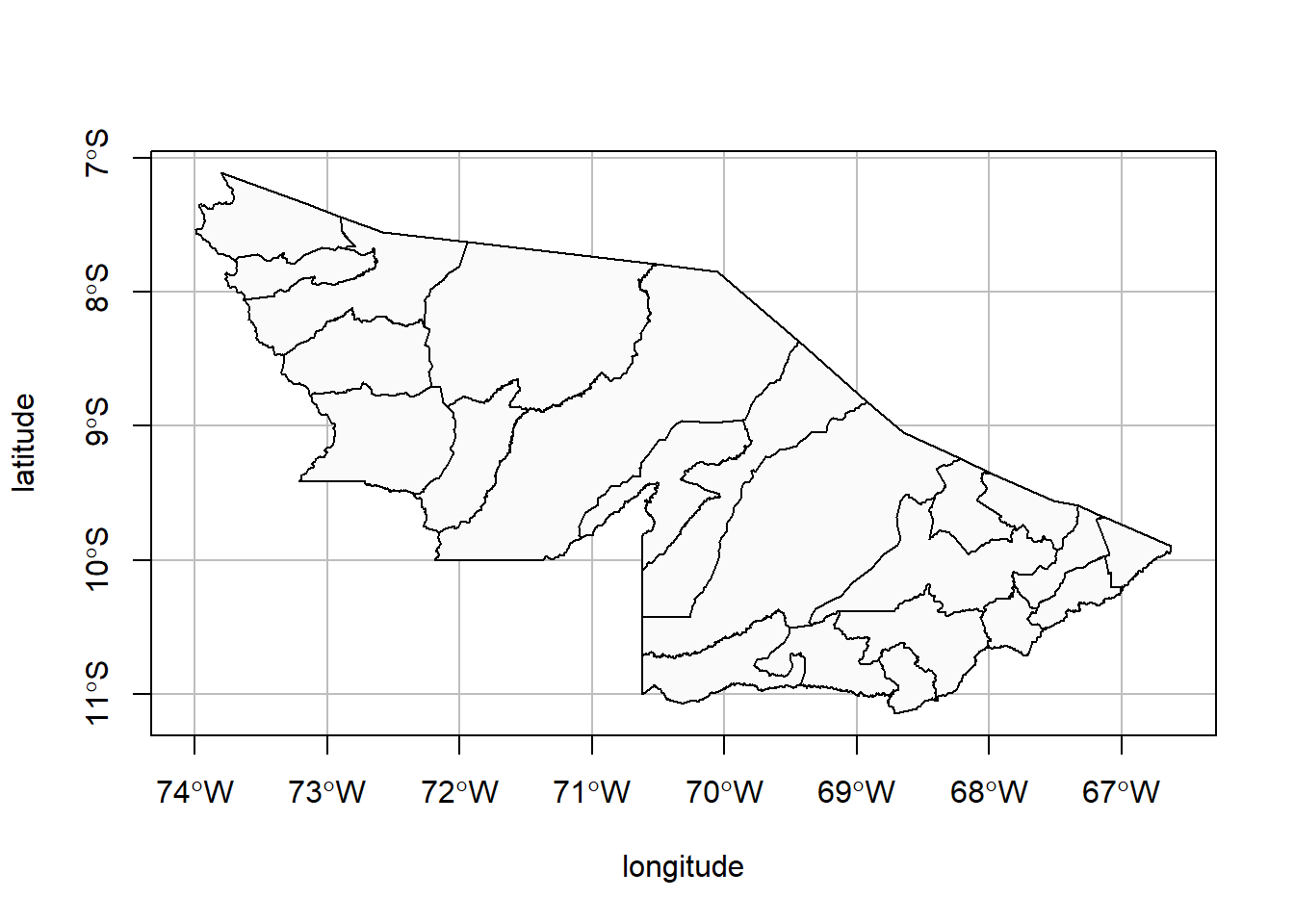
Na Figura 5 vemos, portanto, os municípios do Estado do Acre. Percebe-se que o Estado do Acre se localiza ao extremo oeste do País, dado seu intervalo de longitude (67º a 74º, oeste, representado pela letra W), e no norte do país, dado seu intervalo de latitude (7º a 11º sul, representado pela letra S).

Agora vamos utilizar o pacote ggplot2 para obtermos uma melhor qualidade e finalizar nossa tarefa. Veja em seguida e acompanhe com atenção.

O pacote ggplot2 é um poderoso recurso para visualização de dados. Foi criado por Hadley Wickham e faz parte do universo do tidyverse, um metapacote projetado com a finalidade de apoiar as análises na área de ciência de dados. Esse pacote implementa um sistema de gráficos baseado em uma gramática própria, permitindo a criação de gráficos avançados.

Essa gramática se encarrega de diversos detalhes que precisariam ser especificados se fôssemos usar a função plot() do módulo base do R. Ou seja, é mais fácil de utilizar. Como também é estruturado para sobreposição de camadas, traduz muito bem o comportamento de softwares de informação geográfica. Além disso, integra muito bem com os demais pacotes do tidyverse e possui várias extensões que potencializam seu uso.

Vamos lá! Agora vamos sobrepor as camadas de arquivos importados anteriormente (unidades de saúde, ruas e limites de municípios) para completar nossa tarefa. Para isso, vamos utilizar a função geom_sf() que plota camadas de objetos importados pelo pacote sf. Essa função tem como argumento obrigatório data, que se refere ao objeto sf importado. Vamos utilizar também argumentos estéticos como:

• fill: cor do preenchimento quando o objeto for composto por polígonos e,
• color: cor das linhas e pontos, quando o objeto for compostos por estas geometrias.

Execute o seguinte código no seu computador e observe o mapa que é gerado:

# Utilizando a função ggplot() para plotagem dos mapas
ggplot() +
  
  # Plotando o objeto de polígono com os contornos do estado
  # O argumento "fill" define a cor de preenchimento
  geom_sf(data = ac_municipios, fill = "#FAFAFA") +
  
  # Plotando o objeto de linhas para visualização de estradas
  # O argumento "color" define a cor das linhas
  geom_sf(data = ac_vias, color = "#BABABA") +
  
  # Plotando o objeto de pontos para visualização das unidades de saúde
  # O argumento "color" define a cor de preenchimento
  geom_sf(data = ac_unidades, color = "#FF0000")

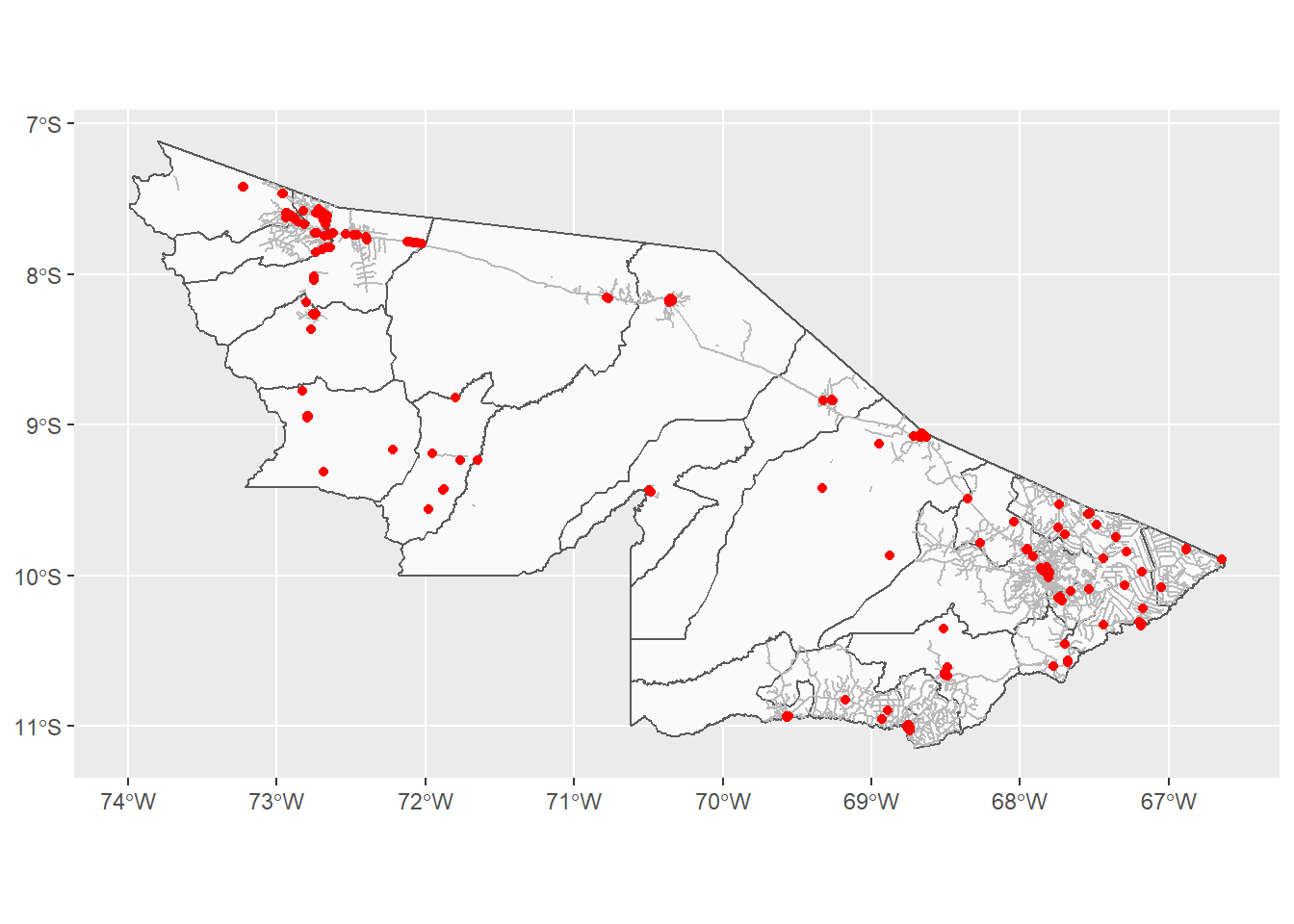
Ficou muito bom, não é mesmo? Está quase pronta nossa tarefa. Perceba que usamos códigos hexadecimais para definir as cores do preenchimento dos polígonos e das ruas. Além disso, o ggplot2 possui um conjunto de configurações contidos em temas que padronizam a cor do fundo e das linhas da latitude e longitude. Alguns dos temas disponíveis são:

• theme_grey() (ou theme_gray()): tema padrão (como o visto acima);
• theme_bw(): uma variação do padrão que usa fundo branco e linhas cinzas;
• theme_linedraw(): um tema com apenas linhas pretas de várias larguras sobre fundo branco;
• theme_light(): semelhante ao anterior, mas com linhas e eixos cinza claro, para dirigir mais atenção para os dados;
• theme_dark(): “o primo escuro” de theme_light(), com linhas de larguras semelhantes, mas com um fundo escuro. Útil para fazer saltar linhas de cores finas;
• theme_minimal(): um tema minimalista, sem anotações ou fundo;
• theme_classic(): Um tema de aspecto “clássico”, com linhas de eixo x e y destacado e nenhuma linha de grade (as linhas internas do gráfico);
• theme_void(): um tema completamente vazio, apresentando somente o mapa.

Vamos utilizar o tema theme_bw() no nosso próximo mapa. Acompanhe com atenção.

Antes de analisarmos o mapa, vamos seguir os padrões cartográficos apresentados neste curso. Agora vamos utilizar o pacote ggspatial para compor os elementos como escala e seta de norte. Para isso, vamos utilizar as funções annotation_scale(), que sobrepõe uma escala gráfica no mapa e annotation_north_arrow(), que sobrepõe uma seta de norte. Os argumentos dessas funções são:

• location: posição do elemento. Neste argumento podem ser usadas as siglas abaixo:
  • tr: top right, acima à direita;
  • tl: top left, acima à esquerda;
  • br: bottom right, abaixo à direita;
  • bl: bottom left, abaixo à esquerda.
• height: altura. Necessário utilizar a função unit() do pacote ggplot2 para especificar a unidade de medida que, no nosso caso, será centímetros;
• style: somente para a seta. É definido um estilo para a seta.

Também vamos utilizar a função labs() do pacote ggplot2 para definir o texto do título (title), do eixo x (no caso, a longitude), do y (no caso, a latitude) e a fonte dos dados.

Para as legendas, vamos utilizar o recurso estético da função aes() do pacote ggplot2 junto com as funções scale_color_manual() e scale_fill_manual(), ambas do mesmo pacote ggplot2. Com a função aes(), podemos definir um codinome para a cor que vamos utilizar nas geometrias (fill e color) e utilizar as demais para formatar rótulos e cores, propriamente ditas.

Execute o código mostrado abaixo com bastante atenção no seu RStudio e observe como fica a composição final do mapa:

# Utilizando a função ggplot() para plotagem dos mapas
ggplot()+
  
  # Adicionando camada com os limites poligonais do estado do AC com o 
  # objeto `ac_municipios` e a função geom_sf().
  # O argumento "fill" define o codinome da cor de preenchimento
  geom_sf(data = ac_municipios, aes(fill = "cor_municipios")) + 
  
  # Adicionando camada com objeto de linhas representando as vias com o 
  # objeto `ac_vias` e a função geom_sf()
  # O argumento "color" define o codinome da cor das linhas
  geom_sf(data = ac_vias, aes(color = "cor_ruas")) +
  
  # Adicionando camada com objeto de pontos  representando unidades de
  # saúde com o objeto `ac_unidades` e a função geom_sf()
  # O argumento "color" define o codinome da cor de preenchimento
  geom_sf(data = ac_unidades, aes(color = "cor_unidades")) +

 # Definindo a escala gráfica do mapa com a função annotation_scale()
  annotation_scale(location = "br",
                   height = unit(.1, "cm")) +
    
  # Definindo a visualização de seta apontada para o Norte  
  annotation_north_arrow(location = "tr",
                         height = unit(1, "cm"),
                         style = north_arrow_fancy_orienteering) +
  
  # Criando a legenda das linhas e pontos
  scale_color_manual(
    name = "",
    guide = guide_legend(override.aes = list(linetype = c("solid", "blank"), 
                                             shape = c(NA, 16))),
    values = c('cor_ruas' = '#BABABA', 'cor_unidades' = '#FF0000'),
    labels = c("Vias", "Unidades de saúde")
  ) +
  
  # Criando a legenda dos polígonos
  scale_fill_manual(
    name = "",
    values = c('cor_municipios' = '#FAFAFA'),
    labels = "Municípios"
  ) +
  
  # Definindo o título e rótulos dos eixos do gráfico  
  labs(title = "Unidades de saúde e arruamento do Estado do Acre, 2022.",
       x = "longitude",
       y = "latitude",
       caption = "Fonte dos dados: IBGE e Ministério da Saúde") +
  
  # Adicionando o tema
  theme_bw()

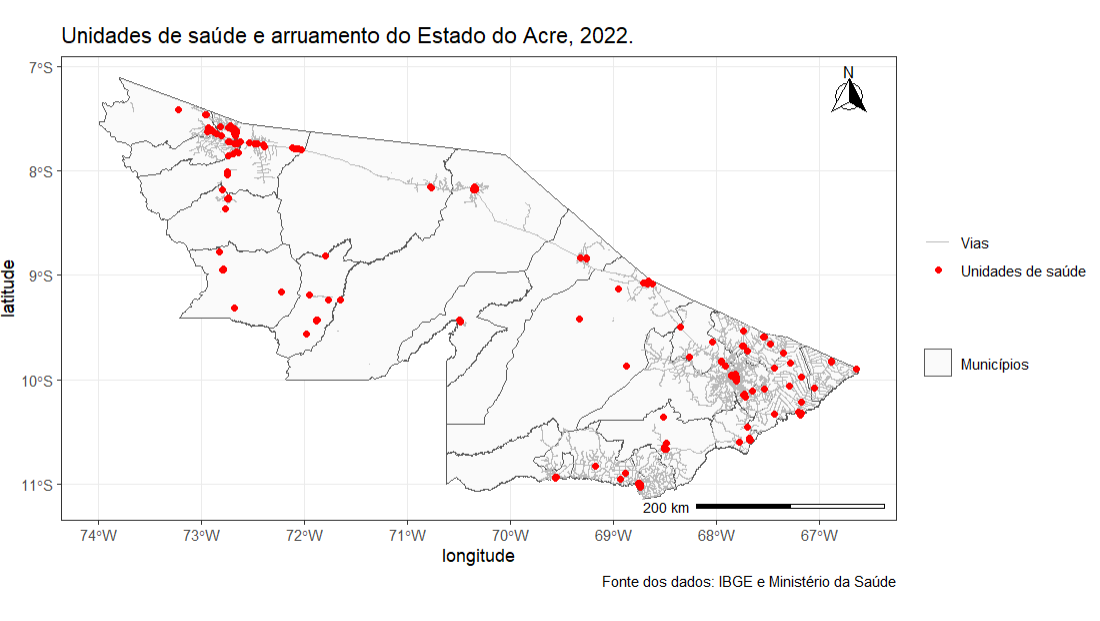
Muito fácil, não é mesmo? Apesar de alguns comandos que podem parecer avançados ou difíceis, com o tempo você se habituará às configurações. O importante é seguir atentamente os códigos apresentados.

Um detalhe que podemos analisar no mapa acima é que, embora a escala utilizada seja para um estado inteiro, impedindo de visualizar detalhes mais próximos, ainda podemos notar as unidades de saúde com uma concentração na região Sul e Sudeste do estado. Nesta região, possivelmente, localizam-se os municípios mais populosos e com maior infraestrutura de saúde disponível, incluindo a capital Rio Branco. Percebemos também que, a Oeste do estado, alguns municípios não possuem estradas de ligação às unidades de saúde. Possivelmente, pode ser unidades localizadas em zona rural ou com acesso somente de barco por rios, dadas algumas características geográficas do Acre.

Vocês perceberam que fizemos uma breve análise somente com os dados que sobrepomos? Essas informações são importantes e podem compor o relatório para apresentar ao diretor geral que solicitou o mapa. Interessante, não é mesmo? Isso demonstra que a capacidade do analista da Vigilância em Saúde pode ir além dos conhecimentos sobre a doença.

Agora vamos entender como cruzar informações de tabelas com os arquivos vetoriais.

Os dados de limites dos municípios podem ser acessados no site do IBGE. Para acessar, acompanhe os passos:

1. acesse no seu navegador www.ibge.gov.br;

2. clique no Menu, em Geociências e, em seguida, em Downloads;

3. siga o seguinte caminho, clicando nas setas da árvore de arquivos:

   ▸ organizacao_do_territorio
   ▸ malhas_territoriais
   ▸ malhas_municipais
   ▸ município_2021
   ▸ Brasil
   ▸ UFs
   

Outra forma de realizar o download dos limites dos municípios, limites dos estados, localização geográfica de unidades de saúde no Brasil, é utilizando o pacote geobr. Esse pacote foi desenvolvido pela equipe do Instituto de Pesquisa Econômica Aplicada (IPEA) e tem como objetivo possibilitar o download de conjuntos oficiais de dados espaciais do Brasil.

Sua utilização é bem simples:

# Instalando e carregando o pacote `geobr`
if(!require(geobr)) install.packages("geobr");
library(geobr)
if(!require(sf)) install.packages("sf");library(sf)

# Realizando o download dos municípios do Estado do Acre
ac_municipios_geobr <- read_municipality("AC")

# Visualizando o objeto `ac_municipios_geobr`
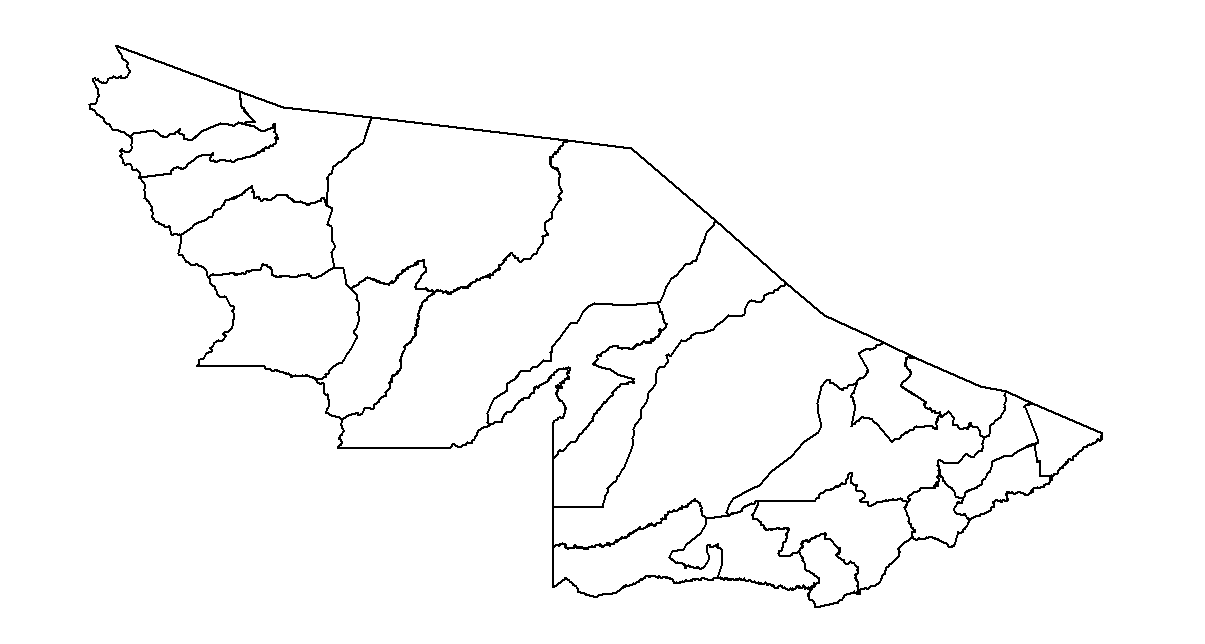
plot(st_geometry(ac_municipios_geobr))

Figura 8: Exemplo de visualização utilizando dados do pacotegeobr.

E por último, uma forma de realizar o download das vias é o pacote osmextract, que baixa dados do projeto Open Street Map.

 # Instalando e carregando o pacote `osmextract`
if(!require(osmextract)) install.packages("osmextract");
library(osmextract)

# Realizando o download dos dados do Estado do Acre
# e filtrando apenas as vias
ac_via_osm <- oe_get(place = "Acre") |> 
  filter(!is.na(highway))
  
# Visualizando o objeto `ac_via_osm`
plot(st_geometry(ac_via_osm))

Figura 9: Exemplo de visualização utilizando dados do pacoteosmextract.